Tunneling escape of waves
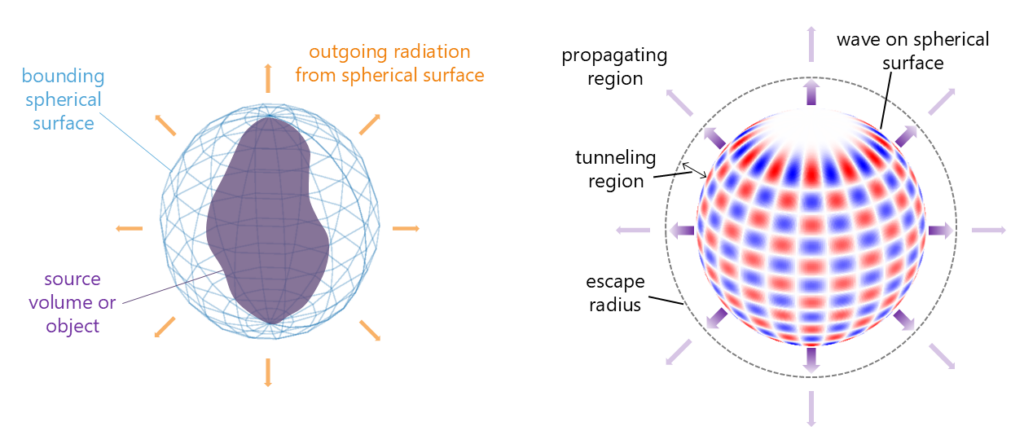
Quite generally, we find empirically that there are only so many orthogonal waves that can usefully propagate out of some volume or from some object. This is seen in experiments and in numerical analyses. After some number of such waves, the coupling strength falls off drastically, in a somewhat exponential fashion, practically limiting this number of useful waves. This behavior is clear for any specific situation we can analyze or calculate, and we usually describe this as corresponding to some “diffraction limit”. However, the physical reason for this fall-off and practical limit has never had a simple explanation, and ideas of “diffraction limits” are not clear for anything other than plane surfaces.
Our approach views any object or volume as being mathematically surrounded by a bounding sphere. Any waves that are to propagate strongly out of the volume would also have to propagate strongly from that sphere. By considering these spherical waves, we show that there is a simple explanation for the fall-off in the coupling strengths of waves: beyond some complexity of the wave on the spherical surface, it has to tunnel to escape. Here by tunneling we mean the quasi-exponential wave process also seen routinely in quantum mechanics. Because of that quasi-exponential behavior, the coupling strength falls off very rapidly. Hence, we have a general explanation for the finite number of well-coupled waves or modes out of any volume, as well as an understanding of the rapid fall-off of coupling strengths. This approach can be used to give a general definition of a diffraction limit, valid for any shape of object or volume.
D. A. B. Miller, Z. Kuang, and O. D. Miller, “Tunneling escape of waves,” Nat. Photon. 19, 284–290 (2025). https://doi.org/10.1038/s41566-024-01578-w Supplementary material





